Hood Design
Problem:
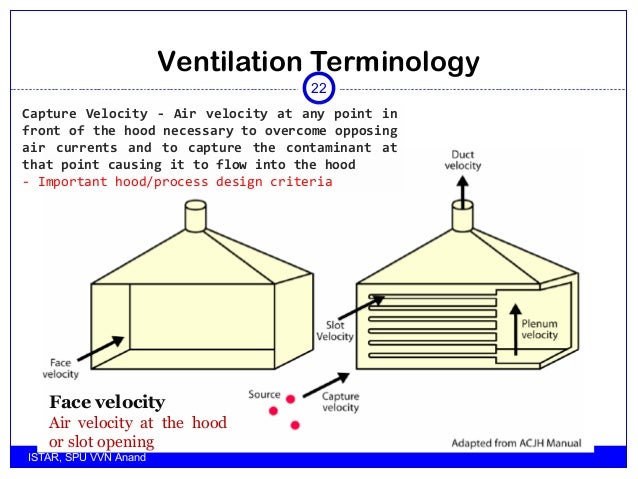
Consider the following hoods:An exterior hood may be an opening on a welding table or slots on the side of a tank. The exterior hood should be located in the path of the emission if transferring larger particulates such as sand. There are four main types of exterior hoods: Canopy: A one- or two-sided overhead hood that receives upward airflow from hot air or gas. Centerline velocity equation for the circular slot hood was thus constructed to design the local exhaust system. Recommended values for airflow rate into the circular slot hood and the average slot face velocity were found to be 20.14 m3/min and 8.55 m/sec, respectively. The optimum air velocity at a. Hood “losses” Minimum duct design velocities. Slotted hoods Slots are used for proper distribution of air across a large area of contamination dispersion. Baffles are the movable partitions used to create slotted openings along the back of the hood. These slots and baffles direct the air that is being exhausted out of the hood. Visible from the working area, the baffles work in concert with the front sash to control airflow and optimize fume hood efficiency.
| Plain opening hood with Ce = 0.82 |
| Flanged opening hood with Ce = 0.76 |
| Cone hood with Ce = 0.93 |
Compute the hood entry loss and percent loss in velocity head for the above case. Comment on your results.
Solution:
Slot hood designs can vary widely. Although variable slot widths offer flexibility, they are subject to tampering. Fixed slots and unobstructed (no internal baffling) plenums are generally the most reliable designs. Plenum velocities are often designed at 1/2 the slot velocity.
Ce = (VPd / SPh)1/2
where Ce is coefficient of entry,
VPd is duct velocity pressure,
SPh is hood static pressure.
SPh = he + VPdwhere he is the hood entry loss.
For plain opening hood,
VPd = SPh * Ce² = 3” * 0.82² = 2.017” wg
he= 3” – 2.017” = 0.983” wg
Percent loss in velocity head = 0.983 / 2.017 = 48.74 %
For flanged opening hood,
VPd = SPh * Ce² = 3” * 0.76² = 1.733” wg
he= 3” – 1.733” = 1.267” wg
Percent loss in velocity head = 1.267 / 1.733 = 73.11 %

For cone hood,
VPd = SPh * Ce² = 3” * 0.93² = 2.595” wg

he= 3” – 2.595” = 0.405” wg
Percent loss in velocity head = 0.405 / 2.595 = 15.61 %
With an increase of Ce, hood entry loss and % loss in velocity decreases.
Cone hood is the better of the three given hoods with only 15% loss in velocity head.Problem:
Find the static pressure of a hood if the velocity pressure is 4.5 'H2O and the coefficient of entry is 0.82.
Solution:

Ce = (VP / SP)1/2
where Ce is coefficient of entry,
VP is velocity pressure,
SP is static pressure.
SP = VP / Ce² = 4.5 / 0.82² = 6.7” of water
Problem:
A 25' wide hood needs a slot velocity of 200 fpm with a 40 cfs volume. What size of slot opening is required?

Solution:
Required area of slot = Q / V = (40 cfs * 60) / (200 fpm) = 12 ft²
Size of slot opening = 12 ft² / (25” / 12) = 5.76 ft = 69.12”
Problem:
Assume the hood static pressure in a 8' duct is 3.0' H2O and the hood manufacturer indicates that Ce is 0.89. What is the estimated flow rate?
Solution:
Hood entry coefficient, Ce = √ (VPduct / SPhood)
So, VPduct = Ce ² * SPhood = 0.89² * 3 = 2.376 “wg
Vduct = 4005 * √VPduct = 6173.42 fpm
Q = Vduct * A = 6173.42 * [π * (8/12)² / 4] = 2154.93 cfm
Problem:
Assume a hood is exhausting 3,000 cfm of air and the hood static pressure was measured at 2.17' w.g. Three months later the hood static pressure is 5.0 ' H2O. Assume continued standard conditions (55oF & 29.92' H2O). Calculate, by how much the air flow through the duct has been reduced?
Solution:
For standard air, Q = 4005 A Ce √ SPhood
For the same hood, Q is proportional to √ SPhood
So, Q2 = Q1 (√ SPhood, 2 / √ SPhood, 1) = 3000 (√ 5 / √ 2.17) = 4553.83 cfm
Increase in air flow rate = (4553.83 – 3000) = 1553.83 cfm
% Increase in air flow rate = (4553.83 – 3000) / 3000 = 51.8 %
Problem:
Compare the flow rate for a lateral hood located at the edge of an open surface tank (4ft*3ft) with the rate for a canopy hood located 3 ft above the tank. The tank contains a solution of ammonium phosphate in water at 250oF. Ammonia gas is released from the tank. State your assumptions.
Solution:
Lateral Hood:
Q = V (10 X² + A)
where, Q = Air Flow (cfm), V = Centerline Velocity at X distance from hood (fpm)
X = Distance of source from edge along axis (ft), A = Area of hood opening (ft²)
Assumptions: Capture Velocity = 75 fpm, Hood Dimensions = 4 ft by 3 ft (same as tank)
V = 75 fpm, X = 0 (hood at edge of tank), A = 4 * 3 = 12 ft²
Q = 75 * 12 = 900cfm
Rectangular Canopy Hood:
Height of hood above tank = 3 ftLow Canopy Hood required.
Q = 6.2 * b1.33 * Δt0.42 * L
where, Q = Air Flow (cfm), b = Width of hood (ft),
Δt = Difference in source and ambient temperature (F), L = Length of hood (ft)
Car Hood Design
Assumptions: Hood Dimensions = 4 ft by 3 ft (same as tank)
b = 3 ft, L = 4 ft, Δt = (250 – 70) = 180 F
Slot Hood Design
Q = 6.2 * 31.33 * 1800.42 * 4 = 946.75 cfm